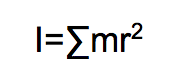Moment of Inertia in Figure Skating
Moment of Inertia is...
- Moment of inertia, or rotational inertia, is the rotational version of mass that acts as a form of resistance. It is written in through the equation:

Left: Above skater with arms out wide has more rotational inertia and less angular velocity, while the skater below with her arms tucked in has less rotational inertia and more angular velocity ---- Right: Figure skater spinning with a low moment of inertia and a higher angular velocity because her arms are pulled in and her leg is crossed
where:
Attached below is a video file that we demonstrated to show how inertia works in figure skating. If the link does not work, right click and open in a new tab to watch.
- I=inertia
- ∑=summation
- m=mass
- r=radius (distance to center)
- In figure skating, rotational inertia takes place as a skater is spinning or jumping because in order to perform the required amount of revolutions spinning on the ice or in the air, they must decrease their moment of inertia. This can be acquired by pulling their arms in closer so they reduce their average radius, or average distance to the center. Since the moment of inertia acts as a form of resistance, a skater can increase their angular velocity (rpm) by reducing their average radius to decrease their moment of inertia. This means that when skaters have their arms out, they have a larger average radius, resulting in a larger moment of inertia and a slower angular velocity. When skaters pull their arms in, they have a smaller average radius, resulting in less rotational inertia and an ability to gain more angular velocity.
Attached below is a video file that we demonstrated to show how inertia works in figure skating. If the link does not work, right click and open in a new tab to watch.
| physics_of_skating_project-moment_of_inertia.mp4 | |
| File Size: | 3984 kb |
| File Type: | mp4 |